Reciprocal lattice란 무엇인가?
오늘은 reciprocal lattice와 물리 공간상에서 격자구조를 기술하는 Bravais lattice, 이 두 가지 격자가 어떻게 다르며, 또 어떻게 연결되어 있는지 알아보겠다.
Reciprocal lattice의 도입은 아래와 같이 간단한 한가지 생각에서 출발했다.
"결정 구조는 특유의 대칭성과 반복성으로 인해 배열구조가 특정 방향을 따라 주기적인 특성을 갖고 있다. 그렇다면, 이 구조가 갖는 물리적인 특성들도 주기성을 띄지 않을까?"주기성 하면 자동으로 떠오르는 것이 파형 아닌가. 따라서 주기성을 염두해 결정구조체의 물성을 이해하고자 하는 시도는 plane wave를 이용해 격자 배열을 기술하는 방식, 즉, reciprocal lattice를 도입하는 것으로 이어졌다. 자, 그럼 이제부터는 천천히 reciprocal lattice의 기술 방식을 살펴보겠다.
우선 파형을 사용하기로 했으니 'k'라는 임의의 wave vector로 기술되는 간단한 plane wave 식을 가져오자.
$$ \Psi_{k}(r) = \Psi_{0} \cdot e^{i \bf{k} \cdot \bf{r}} $$
이 때, 'r'은 임의의 위치벡터이며, 위치 공간 내에 존재하는 이 결정구조의 Bravais lattice는 정의에 따라 아래와 같은 벡터 집합으로 정의되어 있다. 여기서 m, n, o는 정수이며, a1부터 a3 까지의 벡터는 Bravais lattice의 basis vectors이다.
$$ \textbf{R} = m \textbf{a}_{1} + n \textbf{a}_{2} + o \textbf{a}_{3} $$
position vector에 대응하는 Bravais lattice가 'R'이고, wave vector에 대응하는 reciprocal lattice는 'k'이다. (이후에 알 수 있지만, reciprocal lattice도 Bravais lattice임) 각각의 lattice는 불연속적인 공간을 표현하고 있으며, 각 lattice point를 가리키는 벡터들의 집합으로 정의된다.
이제 우리는 앞서 가져온 plane wave function에 대한 wave vectors 'k'의 값을 정의해보고자 한다. 단, 우리에게는 지켜야할 제약조건이 있는데, 바로 이 plane waves가 위치공간(position space)의 Bravais lattice 'R'의 주기성을 그대로 보존해야 한다는 점이다. 이러한 제약조건을 수학적으로 표현하면 다음과 같다.
$$ \Psi( \bf{r}) \stackrel{!}{=} \Psi_{k} ( \bf{r} + \bf{R} ) $$
$$ \Leftrightarrow \Psi_{0} \cdot e^{ i \bf{k} \cdot \bf{r} } = \Psi_{0} \cdot e^{ i \bf{k} ( \bf{r} + \bf{R} ) }$$
Exponential form은 지수가 덧셈일 때, 이것을 분리해 곱으로 표현할 수 있으므로, 두번 째 식은 다시 아래와 같이 정리된다.
$$ \Psi_{0} \cdot e^{ i \bf{k} \cdot \bf{r} } = \Psi_{0} \cdot e^{ i \bf{k} \cdot \bf{r} } \times \Psi_{0} \cdot e^{ i \bf{k} \cdot \bf{R} } $$
$$ \Leftrightarrow \Psi_{0} \cdot e^{ i \bf{k} \cdot \bf{R} } = 1 $$
$$ \Leftrightarrow \textbf{k} \cdot \textbf{R} = 2 \pi l , l \in \Z $$
가장 아래 정리된 식이 만족해야 주기성을 만족시킬 수 있다. 이번에는 이 식을 행렬식으로 표현해보자.
$$ \textbf{R} = m \textbf{a}_{1} + n \textbf{a}_{2} + o \textbf{a}_{3} $$
$$ \textbf{k} = p \textbf{b}_{1} + q \textbf{b}_{2} + r \textbf{b}_{3} $$
$$ \textbf{k} \cdot \textbf{R} = \begin{bmatrix} p & q & r \end{bmatrix} \begin{bmatrix} \textbf{b}_{1} \cdot \textbf{a}_{1} & \textbf{b}_{1} \cdot \textbf{a}_{2} & \textbf{b}_{1} \cdot \textbf{a}_{3} \\ \textbf{b}_{2} \cdot \textbf{a}_{1} & \textbf{b}_{2} \cdot \textbf{a}_{2} & \textbf{b}_{2} \cdot \textbf{a}_{3} \\ \textbf{b}_{3} \cdot \textbf{a}_{1} & \textbf{b}_{3} \cdot \textbf{a}_{2} & \textbf{b}_{3} \cdot \textbf{a}_{3} \end{bmatrix} \begin{bmatrix} m \\ n \\ o \end{bmatrix} = 2 \pi l$$
위의 행렬식은 순전히 주기성 조건에 의해 도출된 식이므로, 우리는 이러한 조건을 만족하는 wave vector 'k'의 basis vector를 임의로 결정해 이 조건을 만족하도록 유도할 수 있다. 간단한 형태로, 아래와 같이 basis를 결정해보자. (이러한 선택이 이후 계산을 매우 편하게 해준다.)
$$ \textbf{a}_{i} \cdot \textbf{b}_{j} = 2 \pi \delta_{ij} $$
그러면, 앞서 살펴본 행력식은 아래와 같이 정리되고, 여기서 새로운 관계식이 도출된다.
$$ \textbf{k} \cdot \textbf{R} = \begin{bmatrix} p & q & r \end{bmatrix} \begin{bmatrix} 2 \pi & 0 & 0 \\ 0 & 2 \pi & 0 \\ 0 & 0 & 2 \pi \end{bmatrix} \begin{bmatrix} m \\ n \\ o \end{bmatrix} = 2 \pi l$$
$$ \textbf{k} \cdot \textbf{R} = pm + qn + ro = l $$
이것은 여전히 우리에게 basis의 정확한 형태를 알려주진 않지만, 아주 중요한 정보를 제공한다. 앞서 위치 공간의 Bravais lattice를 정의할 때 각 basis에 붙는 m, n, o 등을 정수로 하자고 약속했다. 그리고 reciprocal lattice의 주기성 조건 만족을 위한 식에서 l 역시 정수가 되어야 한다고 밝혔다. 따라서 이 두가지 조건을 위 식에 대입하면, 결국 p, q, r 또한 정수가 되어야 한다는 것을 알 수 있다. Reciprocal lattice 또한 하나의 Bravais lattice가 되는 것이다!
자, 이제는 좀더 구체적으로 basis를 어떻게 정할 수 있는지 알아보자. 우리가 도입한 조건에 따르면 (위의 행렬식을 보라), 다음 두 개 조건이 유효하다는 것을 알 수 있다.
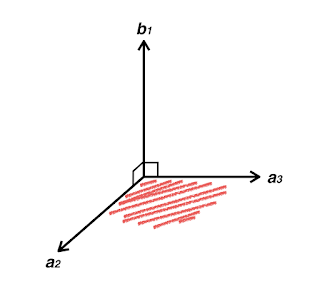
$$ \textbf{b}_{1} \cdot \textbf{a}_{2} = 0 $$
$$ \textbf{b}_{1} \cdot \textbf{a}_{3} = 0 $$
$$ \textbf{b}_{1} = c (\textbf{a}_{2} \times \textbf{a}_{3}) $$
이것을 앞서 살펴봤던 아래의 조건 식에 넣으면,
$$ \textbf{a}_{1} \cdot \textbf{b}_{1} = 2 \pi \delta_{11} = 2 \pi$$
$$ \Rightarrow \textbf{a}_{1} \cdot \textbf{b}_{1} = c \textbf{a}_{1} \cdot (\textbf{a}_{2} \times \textbf{a}_{3}) = 2 \pi $$
$$ \Rightarrow c = \frac{2 \pi}{\textbf{a}_{1} \cdot (\textbf{a}_{2} \times \textbf{a}_{3})}$$
$$ V_{parallelpiped} := \textbf{a}_{1} \cdot ( \textbf{a}_{2} \times \textbf{a}_{3} ) $$
우리는 위에서 상수 'c'의 값을 찾아냈으며, 덕분에 이제 위치 공간 상의 Bravais lattice basis 들을 이용해 reciprocal lattice basis를 찾아낼 수 있게 됐다. 흥미로운 점은 상수 'c'의 값이 plane wave의 주기 하나를 의미하는 2 pi를 basis vector들이 만드는 부피(parallelpiped)로 나눈 값이라는 것이다. 이것은 primitive cell을 정할 때 하나의 cell 안에 원자가 하나 포함되도록 했던 것을 떠오르게 한다.
어쨌거나 이렇게 찾아낸 'c'값을 이용하면 다음과 같이 basis를 정할 수 있다.
$$ \textbf{b}_{1} = 2 \pi \cdot \frac{ \textbf{a}_{2} \times \textbf{a}_{3} }{V} $$
$$ \textbf{b}_{2} = 2 \pi \cdot \frac{ \textbf{a}_{3} \times \textbf{a}_{1} }{V} $$
$$ \textbf{b}_{3} = 2 \pi \cdot \frac{ \textbf{a}_{1} \times \textbf{a}_{2} }{V} $$
Comments
Post a Comment